Finite-State Automata and Regular Languages

(Content adapted from Critchlow & Eck)

We know now that our two models for mechanical language recognition actually recognize the same class of languages. The question still remains: do they recognize the same class of languages as the class generated mechanically by regular expressions? The answer turns out to be "yes". There are two parts to proving this: first that every language generated can be recognized, and second that every language recognized can be generated.

Regular Expression to NFA

Theorem: Every language generated by a regular expression can be recognized by an NFA.

Proof: The proof of this theorem is a nice example of a proof by induction on the structure of regular expressions. The definition of regular expression is inductive: $\Phi$, $\varepsilon$, and $a$ are the simplest regular expressions, and then more complicated regular expressions can be built from these. We will show that there are NFAs that accept the languages generated by the simplest regular expressions, and then show how those machines can be put together to form machines that accept languages generated by more complicated regular expressions.

Consider the regular expression $\Phi$. $L(\Phi) = \{\}$. Here is a machine that accepts $\{\}$:

Consider the regular expression $\varepsilon$. $L(\varepsilon) = \{\varepsilon\}$. Here is a machine that accepts $\{\varepsilon\}$:

Consider the regular expression $a$. $L(a) = \{a\}$. Here is a machine that accepts $\{a\}$:

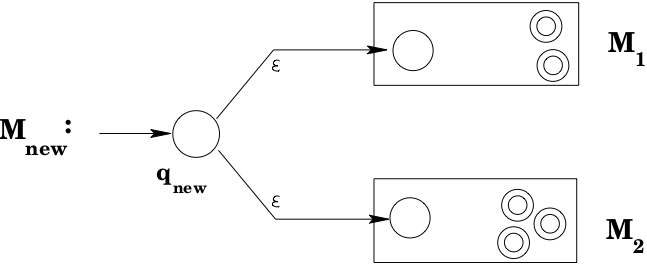
Now suppose that you have NFAs that accept the languages generated by the regular expressions $r_1$ and $r_2$. Building a machine that accepts $L(r_1 | r_2)$ is fairly straightforward: take an NFA $M_1$ that accepts $L(r_1)$ and an NFA $M_2$ that accepts $L(r_2)$. Introduce a new state $q_{new}$, connect it to the start states of $M_1$ and $M_2$ via $\varepsilon$-transitions, and designate it as the start state of the new machine. No other transitions are added. The final states of $M_1$ together with the final states of $M_2$ are designated as the final states of the new machine. It should be fairly clear that this new machine accepts exactly those strings accepted by $M_1$ together with those strings accepted by $M_2$: any string $w$ that was accepted by $M_1$ will be accepted by the new NFA by starting with an $\varepsilon$-transition to the old start state of $M_1$ and then following the accepting path through $M_1$; similarly, any string accepted by $M_2$ will be accepted by the new machine; these are the only strings that will be accepted by the new machine, as on any input $w$ all the new machine can do is make an $\varepsilon$-move to $M_1$'s (or $M_2$'s) start state, and from there $w$ will only be accepted by the new machine if it is accepted by $M_1$ (or $M_2$). Thus, the new machine accepts $L(M_1) \cup L(M_2)$, which is $L(r_1) \cup L(r_2)$, which is exactly the definition of $L(r_1 | r_2)$.

(A pause before we continue: note that for the simplest regular expressions, the machines that we created to accept the languages generated by the regular expressions were in fact DFAs. In our last case above, however, we needed $\varepsilon$-transitions to build the new machine, and so if we were trying to prove that every regular language could be accepted by a DFA, our proof would be in trouble. THIS DOES NOT MEAN that the statement "every regular language can be accepted by a DFA" is false, just that we can't prove it using this kind of argument, and would have to find an alternative proof.)

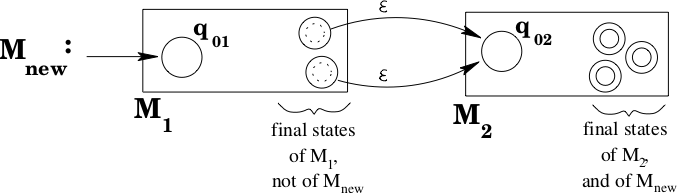
Suppose you have machines $M_1$ and $M_2$ that accept $L(r_1)$ and $L(r_2)$ respectively. To build a machine that accepts $L(r_1)L(r_2)$ proceed as follows. Make the start state $q_{01}$ of $M_1$ be the start state of the new machine. Make the final states of $M_2$ be the final states of the new machine. Add $\varepsilon$-transitions from the final states of $M_1$ to the start state $q_{02}$ of $M_2$.

It should be fairly clear that this new machine accepts exactly those strings of the form $xy$ where $x\in L(r_1)$ and $y \in L(r_2)$: first of all, any string of this form will be accepted because $x\in L(r_1)$ implies there is a path that consumes $x$ from $q_{01}$ to a final state of $M_1$; a $\varepsilon$-transition moves to $q_{02}$; then $y \in L(r_2)$ implies there is a path that consumes $y$ from $q_{02}$ to a final state of $M_2$; and the final states of $M_2$ are the final states of the new machine, so $xy$ will be accepted. Conversely, suppose $z$ is accepted by the new machine. Since the only final states of the new machine are in the old $M_2$, and the only way to get into $M_2$ is to take a $\varepsilon$-transition from a final state of $M_1$, this means that $z=xy$ where $x$ takes the machine from its start state to a final state of $M_1$, a $\varepsilon$-transition occurs, and then $y$ takes the machine from $q_{02}$ to a final state of $M_2$. Clearly, $x\in L(r_1)$ and $y \in L(r_2)$.

We leave the construction of an NFA that accepts $L(r^*)$ from an NFA that accepts $L(r)$ as an exercise.

The algorithm in this proof is commonly known as Thompson's Construction, credited to Ken Thompson who, along with Dennis Ritchie, also designed and implemented Unix and the C programming language.¹ Several of the utilities that Thompson developed for Unix, such as ed and grep, make use of regular expressions for searching and replacing text.

NFA to Regular Expression

Theorem: Every language that is accepted by a DFA or an NFA is generated by a regular expression.

Proving this result is actually fairly involved and not very illuminating. Before presenting a proof, we will give an illustrative example of how one might actually go about extracting a regular expression from an NFA or a DFA. You can go on to read the proof if you are interested.

---

Example: Consider the DFA shown below:

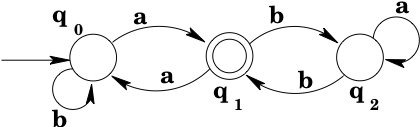
Note that there is a loop from state $q_2$ back to state $q_2$: any number of $a$'s will keep the machine in state $q_2$, and so we label the transition with the regular expression $a^*$. We do the same thing to the transition labeled $b$ from $q_0$. (Note that the result is no longer a DFA, but that doesn't concern us, we're just interested in developing a regular expression.)

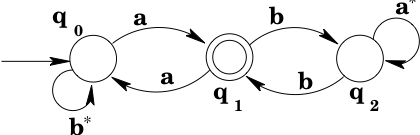
Next we note that there is in fact a loop from $q_1$ to $q_1$ via $q_0$. A regular expression that matches the strings that would move around the loop is $ab^*a$. So we add a transition labeled $ab^*a$ from $q_1$ to $q_1$, and remove the now-irrelevant $a$-transition from $q_1$ to $q_0$. (It is irrelevant because it is not part of any other loop from $q_1$ to $q_1$.)

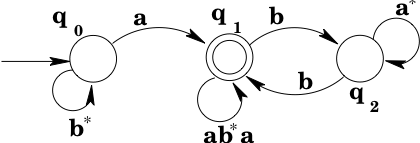
Next we note that there is also a loop from $q_1$ to $q_1$ via $q_2$. A regular expression that matches the strings that would move around the loop is $ba^*b$. Since the transitions in the loop are the only transitions to or from $q_2$, we simply remove $q_2$ and replace it with a transition from $q_1$ to $q_1$.

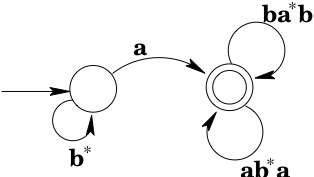
It is now clear from the diagram that strings of the form $b^*a$ get you to state $q_1$, and any number of repetitions of strings that match $ab^*a$ or $ba^*b$ will keep you there. So the machine accepts $L(b^*a(ab^*a | ba^*b)^*)$.

---

Proof: We prove that the language accepted by a DFA is regular. The proof for NFAs follows from the equivalence between DFAs and NFAs.

Suppose that $M$ is a DFA, where $M=(Q,\Sigma,q_0,\delta,F)$. Let $n$ be the number of states in $M$, and write $Q=\{q_0,q_1,\dots,q_{n-1}\}$. We want to consider computations in which $M$ starts in some state $q_i$, reads a string $w$, and ends in state $q_k$. In such a computation, $M$ might go through a series of intermediates states between $q_i$ and $q_k$: $q_i\longrightarrow p_1\longrightarrow p_2 \cdots\longrightarrow p_r\longrightarrow q_k$ We are interested in computations in which all of the intermediate states—$p_1,p_2,\dots,p_r$—are in the set $\{q_0,q_1,\dots,q_{j-1}\}$, for some number $j$. We define $R_{i,j,k}$ to be the set of all strings $w$ in $\Sigma^*$ that are consumed by such a computation. That is, $w\in R_{i,j,k}$ if and only if when $M$ starts in state $q_i$ and reads $w$, it ends in state $q_k$, and all the intermediate states between $q_i$ and $q_k$ are in the set $\{q_0,q_1,\dots,q_{j-1}\}$. $R_{i,j,k}$ is a language over $\Sigma$. We show that $R_{i,j,k}$ for $0\le i < n$, $0\le j \le n$, $0\le k < n$.

Consider the language $R_{i,0,k}$. For $w\in R_{i,0,k}$, the set of allowable intermediate states is empty. Since there can be no intermediate states, it follows that there can be at most one step in the computation that starts in state $q_i$, reads $w$, and ends in state $q_k$. So, $|w|$ can be at most one. This means that $R_{i,0,k}$ is finite, and hence is regular. (In fact, $R_{i,0,k}=\{a\in\Sigma\,|\, \delta(q_i,a)=q_k\}$, for $i\ne k$, and $R_{i,0,i}=\{\varepsilon\}\cup\{a\in\Sigma\,|\, \delta(q_i,a)=q_i\}$. Note that in many cases, $R_{i,0,k}$ will be the empty set.)

We now proceed by induction on $j$ to show that $R_{i,j,k}$ is regular for all $i$ and $k$. We have proved the base case, $j=0$. Suppose that $0\le j< n$ we already know that $R_{i,j,k}$ is regular for all $i$ and all $k$. We need to show that $R_{i,j+1,k}$ is regular for all $i$ and $k$. In fact, $R_{i,j+1,k}=R_{i,j,k}\cup \left( R_{i,j,j}R_{j,j,j}^*R_{j,j,k}\right)$ which is regular because $R_{i,j,k}$ is regular for all $i$ and $k$, and because the union, concatenation, and Kleene star of regular languages are regular.

To see that the above equation holds, consider a string $w\in\Sigma^*$. Now, $w\in R_{i,j+1,k}$ if and only if when $M$ starts in state $q_i$ and reads $w$, it ends in state $q_k$, with all intermediate states in the computation in the set $\{q_0,q_1,\dots,q_j\}$. Consider such a computation. There are two cases: Either $q_j$ occurs as an intermediate state in the computation, or it does not. If it does not occur, then all the intermediate states are in the set $\{q_0,q_1,\dots,q_{j-1}\}$, which means that in fact $w\in R_{i,j,k}$. If $q_j$ does occur as an intermediate state in the computation, then we can break the computation into phases, by dividing it at each point where $q_j$ occurs as an intermediate state. This breaks $w$ into a concatenation $w=xy_1y_2\cdots y_rz$. The string $x$ is consumed in the first phase of the computation, during which $M$ goes from state $q_i$ to the first occurrence of $q_j$; since the intermediate states in this computation are in the set $\{q_0,q_1,\dots,q_{j-1}\}$, $x\in R_{i,j,j}$. The string $z$ is consumed by the last phase of the computation, in which $M$ goes from the final occurrence of $q_j$ to $q_k$, so that $z\in R_{j,j,k}$. And each string $y_t$ is consumed in a phase of the computation in which $M$ goes from one occurrence of $q_j$ to the next occurrence of $q_j$, so that $y_r\in R_{j,j,j}$. This means that $w=xy_1y_2\cdots y_rz\in R_{i,j,j}R_{j,j,j}^*R_{j,j,k}$.

We now know, in particular, that $R_{0,n,k}$ is a regular language for all $k$. But $R_{0,n,k}$ consists of all strings $w\in\Sigma^*$ such that when $M$ starts in state $q_0$ and reads $w$, it ends in state $q_k$ (with no restriction on the intermediate states in the computation, since every state of $M$ is in the set $\{q_0,q_1,\dots,q_{n-1}\}$). To finish the proof that $L(M)$ is regular, it is only necessary to note that $L(M)=\bigcup_{q_k\in F} R_{0,n,k}$ which is regular since it is a union of regular languages. This equation is true since a string $w$ is in $L(M)$ if and only if when $M$ starts in state $q_0$ and reads $w$, in ends in some accepting state $q_k\in F$. This is the same as saying $w\in R_{0,n,k}$ for some $k$ with $q_k\in F$.

Closure Properties for Regular Languages

We have already seen that if two languages $L_1$ and $L_2$ are regular, then so are $L_1 \cup L_2$, $L_1L_2$, and $L_1^*$ (and of course $L_2^*$). We have not yet seen, however, how the common set operations intersection and complementation affect regularity. Is the complement of a regular language regular? How about the intersection of two regular languages?

Both of these questions can be answered by thinking of regular languages in terms of their acceptance by DFAs. Let's consider first the question of complementation. Suppose we have an arbitrary regular language $L$. We know there is a DFA $M$ that accepts $L$. Pause a moment and try to think of a modification that you could make to $M$ that would produce a new machine $M'$ that accepts $\overline{L}$…. Okay, the obvious thing to try is to make $M'$ be a copy of $M$ with all final states of $M$ becoming non-final states of $M'$ and vice versa. This is in fact exactly right: $M'$ does in fact accept $\overline{L}$. To verify this, consider an arbitrary string $w$. The transition functions for the two machines $M$ and $M'$ are identical, so $\delta^* (q_0, w)$ is the same state in both $M$ and $M'$; if that state is accepting in $M$ then it is non-accepting in $M'$, so if $w$ is accepted by $M$ it is not accepted by $M'$; if the state is non-accepting in $M$ then it is accepting in $M'$, so if $w$ is not accepted by $M$ then it is accepted by $M'$. Thus $M'$ accepts exactly those strings that $M$ does not, and hence accepts $\overline{L}$.

It is worth pausing for a moment and looking at the above argument a bit longer. Would the argument have worked if we had looked at an arbitrary language $L$ and an arbitrary NFA $M$ that accepted $L$? That is, if we had built a new machine $M'$ in which the final and non-final states had been switched, would the new NFA $M'$ accept the complement of the language accepted by $M$? The answer is "not necessarily". Remember that acceptance in an NFA is determined based on whether or not at least one of the states reached by a string is accepting. So any string $w$ with the property that $\partial^*(q_0, w)$ contains both accepting and non-accepting states of $M$ would be accepted both by $M$ and by $M'$.

Now let's turn to the question of intersection. Given two regular languages $L_1$ and $L_2$, is $L_1 \cap L_2$ regular? Again, it is useful to think in terms of DFAs: given machines $M_1$ and $M_2$ that accept $L_1$ and $L_2$, can you use them to build a new machine that accepts $L_1 \cap L_2$? The answer is yes, and the idea behind the construction bears some resemblance to that behind the NFA-to-DFA construction. We want a new machine where transitions reflect the transitions of both $M_1$ and $M_2$ simultaneously, and we want to accept a string $w$ only if those sequences of transitions lead to final states in both $M_1$ and $M_2$. So we associate the states of our new machine $M$ with pairs of states from $M_1$ and $M_2$. For each state $(q_1,q_2)$ in the new machine and input symbol $a$, define $\delta((q_1,q_2),a)$ to be the state $(\delta_1(q_1,a), \delta_2(q_2,a))$. The start state $q_0$ of $M$ is $(q_{01}, q_{02})$, where $q_{0i}$ is the start state of $M_i$. The final states of $M$ are the the states of the form $(q_{f1}, q_{f2})$ where $q_{f1}$ is an accepting state of $M_1$ and $q_{f2}$ is an accepting state of $M_2$. You should convince yourself that $M$ accepts a string $x$ iff $x$ is accepted by both $M_1$ and $M_2$.

The results of the previous section and the preceding discussion are summarized by the following theorem:

Theorem: The intersection of two regular languages is a regular language.

The union of two regular languages is a regular language.

The concatenation of two regular languages is a regular language.

The complement of a regular language is a regular language.

The Kleene closure of a regular language is a regular language.

Exercises

1. Give a DFA that accepts the intersection of the languages accepted by the machines shown below. (Suggestion: use the construction discussed just before the previous theorem.)

2. Complete Thompson's Construction by showing how to modify a machine that accepts $L(r)$ into a machine that accepts $L(r^*)$.

3. Using Thompson's Construction, build an NFA that accepts $L((ab | a)^*(bb))$.

4. Prove that the reverse of a regular language is regular.

   Answer

   Given a DFA for the language, construct an NFA by reversing all of the edges. The original start state should become the only final state, and there should be a new start state with $\varepsilon$-transitions to each of the original final states. If there is an accepting path from this new start state to the final state, then it must correspond to the reverse of an accepting path in the original machine. Therefore, the new NFA will accept exactly the reverse of the given regular langauge.

5. Show that for any DFA or NFA, there is an NFA with exactly one final state that accepts the same language.

   Answer

   Define the NFA by adding one new state. This state should be the only final state, and all of the original final states should instead have $\varepsilon$-transitions to the new state.

6. Suppose we change the model of NFAs to allow NFAs to have multiple start states. Show that for any "NFA" with multiple start states, there is an NFA with exactly one start state that accepts the same language.

   Answer

   Given such an extended NFA, define an ordinary NFA by adding a new state. This state should be the only start state, and it should have $\varepsilon$-transitions to each of the original start states.

7. Show that the closure of regular languages under both union and complement is enough to show that they are also closed under intersection.

   Answer

   This is just an application of DeMorgan's laws: $L_1\cap L_2 = \overline{\overline{L_1}\cup\overline{L_2}}$.

---

1. Thompson is actually credited with creating B, while Ritchie created its successor C.↩